EdisonでOpenRTM-aist(実装編)

さて前回述べた通りSainSmart製4自由度ロボットアームの制御をEdisonでやろうと思います。
と思ったのですが、ロボットアームを持っていません。
動いている動画を見つけたので、どういう動作なのか見てみます。



一見、こんな感じのシリアルリンク機構ですが、



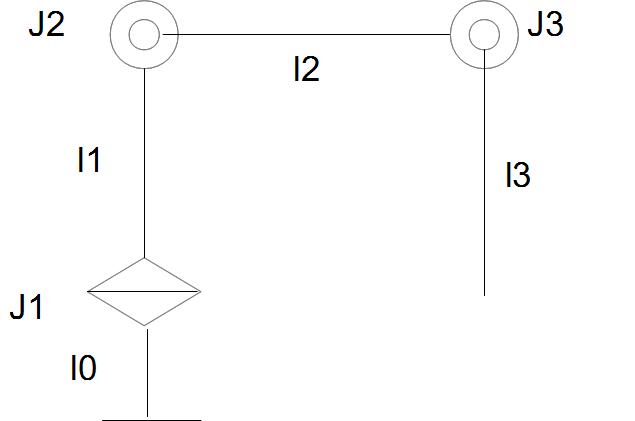
実際はこんな感じです。

 

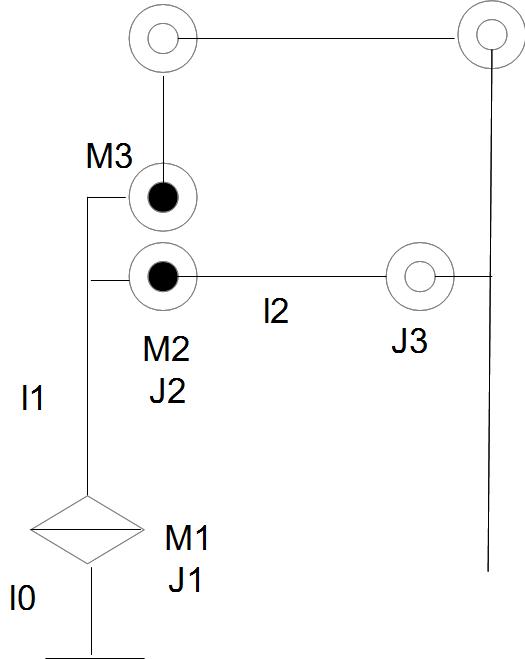
本当はM2とM3が重なっていたり、J3とL3が重なっていたりするのですが、図の見やすさからこうしてます。実際は以下のような配置です。




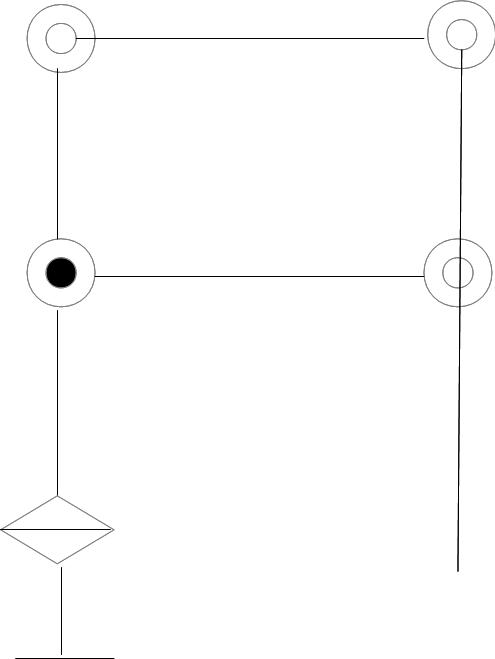
他にも部品がじゃらじゃら付いていますが手先を地面と平行にするためのものだと思います。


一応、座標系は以下のように設定します。





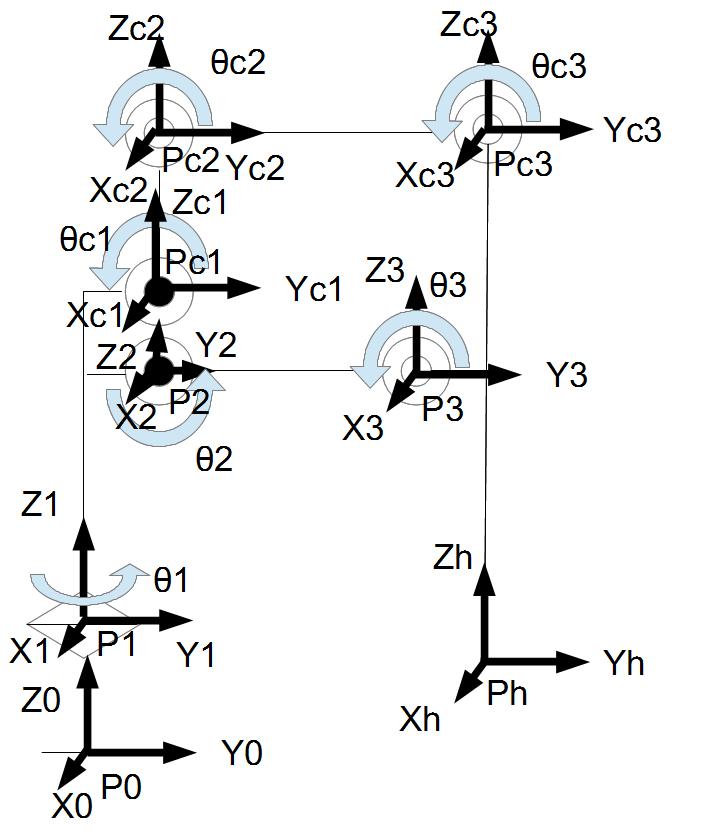
後、モーターの角度はθm1、θm2、θm3とします。

とりあえず逆運動学で手先位置から関節角度、さらにそこからモーターの角度を求めたいのでまずはモーターの角度と関節角度の関係を求めます。
θ1=θm1、θ2=θm2は見たまんまなのですが、θ3が一見すると難しそうです。
と思わせておいて、M2とM3、J3とL3が重なっており、向かい合うリンクの長さが同じ場合は簡単です。
とりあえず、一部だけ抜き出して簡略化してみます。

  



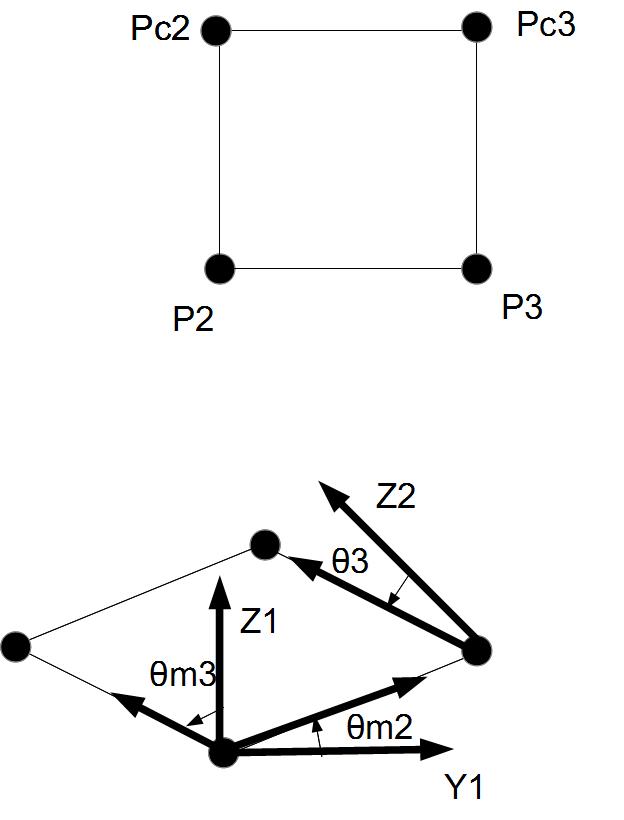
このように常に向かい合うリンクが平行になるので、θ3はθm3からθm2を引いただけで導出できます。
つまりモーターの角度と関節角度の関係式は以下のようになります。



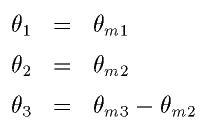
次に手先位置を関節角度から順運動学で導出します。
計算過程は省きますが以下のようになります。
 
 
  
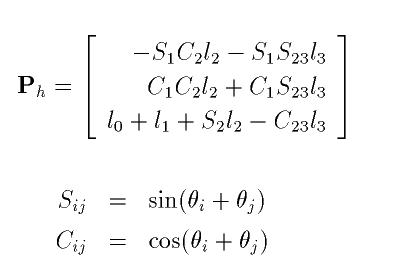
そしてここから偏微分して手先速度と関節角速度の関係を求め、ヤコビ行列を導出します。
以下のように導出できます。





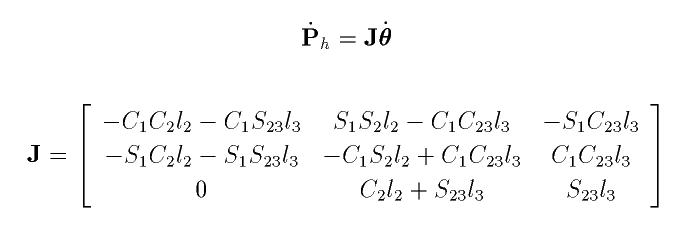
後は逆ヤコビ行列を導出して手先速度を入力すれば関節角速度が求まります。

次に手先の軌道を考えます。
とりあえず、初期位置と目標位置との距離ST、到達時間T、時間tから以下の式のように三角関数で導出します。



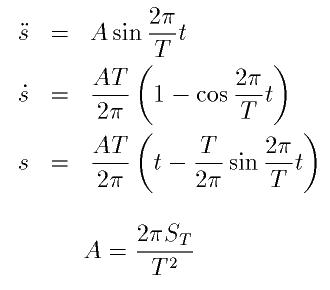
ちなみにこの計算式では以下のような軌道になります 。




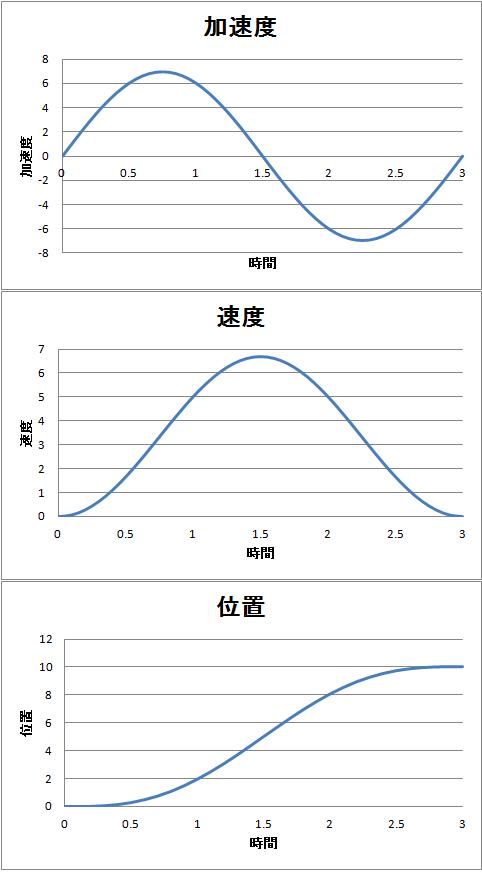
急に加減速したら恐いので滑らかな軌道を描くようにしましょう。


この式から先端の目標加速度、速度、位置は以下の式で導出できます。

 

 
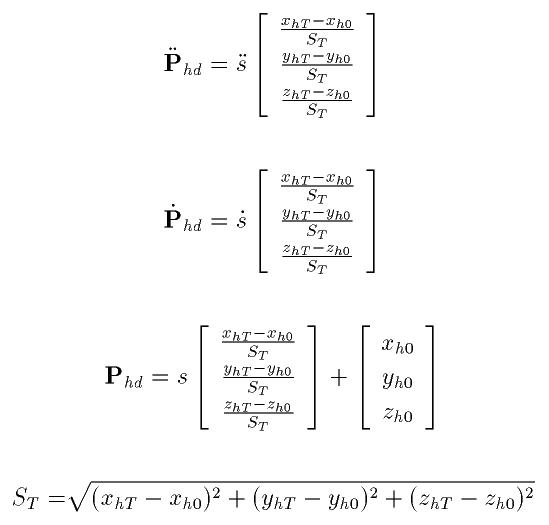
そして位置誤差のフィードバックを加えて先端指令速度を導出して、そこから関節角速度、関節角度を導出できます。



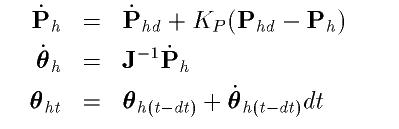
おそらく角加速度をセンシングする手段はないのでdθhで導出した関節角速度の指令値をそのまま積分します。


これで分解速度制御を行うために必要な数式は一通り導出できたので、ODEでシミュレーションを行います。ChoreonoidとかV-REPとか使わないのかよとか言われそうですが、あまりそういう気分でもないのでやめておきます。そりゃできればあの機構でシミュレーションをやりたいのですが、難しいので簡略化したモデルでシミュレーションしています。
動画は作っていないので、見たい人はここからシミュレーションのソースコードと実行ファイルをダウンロードしてください。



目標位置に手先が滑らかに移動できています。


と言うか、僕は何で持ってもいないロボットの制御則を考えているのでしょうね？
何だか悲しくなってきました。



次はここからどのようにRTCを設計するかを考えてみます。











にほんブログ村のロボットのカテゴリから
全然人が来ない・・・